问题
填空题
已知∠AOB=30°,点P在∠AOB的内部,OP=a,若OA上有一动点M,OB上有一动点N,则△PMN的最小周长为______.(结果用含a的式子表示)
答案
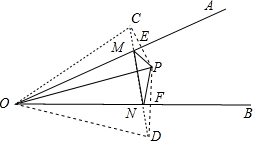
作P关于直线OA的对称点C,作P关于直线OB的对称点D,连接CD,交AB于M,交OB于N,
则此时△PMN的周长最小,
连接OC,OD,
∵P关于直线OA的对称点C,P关于直线OB的对称点D,
∴CM=PM,PN=ND,∠COE=∠POE,∠POF=∠DOF,OC=OP=OD=a,
∵∠POM+∠PON=∠AOB=30°,
∴∠COD=∠COE+∠POE+∠DOF+∠POF=30°+30°=60°,
∴△COD是等边三角形,
∴CD=OC=OD=a,
即△PMN的周长的最小值是PM+MN+PN=CM+MN+DN=CD=a,
故答案为:a.