问题
选择题
设a∈R，若函数y=ex+ax，x∈R，有大于零的极值点，则（ ）
|
答案
解：∵y=ex+ax，
∴y'=ex+a．由题意知ex+a=0有大于0的实根，
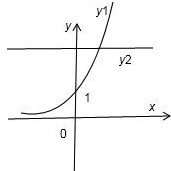
令y1=ex，y2=-a，则两曲线交点在第一象限，结合图象易得-a＞1?a＜-1，
故选A．
搜题请搜索小程序“爱下问搜题”
设a∈R，若函数y=ex+ax，x∈R，有大于零的极值点，则（ ）
|
解：∵y=ex+ax，
∴y'=ex+a．由题意知ex+a=0有大于0的实根，
令y1=ex，y2=-a，则两曲线交点在第一象限，结合图象易得-a＞1?a＜-1，
故选A．