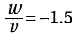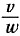问题
解答题
设集合A={x|
（1）求A∩Z； （2）若A⊇B，求m的取值范围． |
答案
（1）对于A，化简可得，
≤1 32
x≤41 2
由指数的性质，可得-2≤x≤5；
集合A={x|-2≤x≤5}，
则A∩Z={-2、-1、0、1、2、3、4、5}；
（2）根据题意，集合B={x|（x-m+1）（x-2m-1）＜0}；
方程（x-m+1）（x-2m-1）=0有2根，即（m-1）与（2m+1）；
分情况讨论可得：
①当m=-2时，b=∅，所以B⊆A；
②当m＜-2时，（2m+1）-（m-1）＜0，
所以B=（2m+1，m-1），
因此，要以B⊆A，则只要
，2m+1≥-2 m-1≤5
解可得，-
≤m≤6，所以m的值不存在；3 2
③当m＞-2时，（2m+1）-（m-1）＞0，
所以B=（m-1，2m+1），
因此，要以B⊆A，，则只要
，m-1≥-2 2m+1≤5
解可得：-1≤m≤2．
综上所述，知m的取值范围是：m=-2或-1≤m≤2．