问题
单项选择题
设曲线y=f(x)在原点处与y=sinx相切,a,b为常数,且ab≠0,则
 等于( )
等于( )
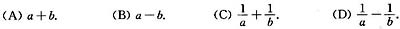
答案
参考答案:A
解析:
[分析]: 已知两曲线在原点处相切,相当于已知对应的两函数在x=0处具有相同的函数值与导数值。
[详解] 由所给条件知:f(0)=0,f'(0)=(sinx)'|x=0=1,
于是[*]
故应选(A)
[评注] 此题属常规题,主要考查按定义求导数。
设曲线y=f(x)在原点处与y=sinx相切,a,b为常数,且ab≠0,则
 等于( )
等于( )
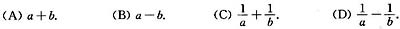
参考答案:A
解析:
[分析]: 已知两曲线在原点处相切,相当于已知对应的两函数在x=0处具有相同的函数值与导数值。
[详解] 由所给条件知:f(0)=0,f'(0)=(sinx)'|x=0=1,
于是[*]
故应选(A)
[评注] 此题属常规题,主要考查按定义求导数。