问题
选择题
函数f（x）=ln2x+2lnx+2的极小值为（ ）
|
答案
解：令f′（x）=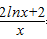
=0，解得x=e-1，又函数f（x）的定义域为（0，+∞），
当x变化时，f（x）及f′（x）的变化情况如下表：
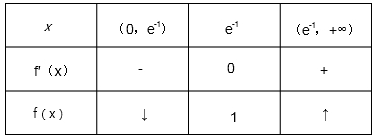
所以得到函数f（x）的极小值为f（e-1）=（lne-1）2+2lne-1+2=1-2+2=1．
故选D
搜题请搜索小程序“爱下问搜题”
函数f（x）=ln2x+2lnx+2的极小值为（ ）
|
解：令f′（x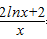）==0，解得x=e-1，又函数f（x）的定义域为（0，+∞），
当x变化时，f（x）及f′（x）的变化情况如下表：
所以得到函数f（x）的极小值为f（e-1）=（lne-1）2+2lne-1+2=1-2+2=1．
故选D