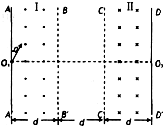
如图所示,矩形区域I和II内分别存在方向垂直于纸面向外和向里的匀强磁场(AA′、BB′、CC′、DD′为磁场边界,四者相互平行),磁感应强度大小均为B,矩形区域的长度足够长,两磁场宽度及BB′与CC′之间的距离均相同.某种带正电的粒子从AA′上O1处以大小不同的速度沿与O1A成α=30°角进入磁场(如图所示,不计粒子所受重力),当粒子的速度小于某一值时,粒子在区域I内的运动时间均为t0.当速度为v0时,粒子在区域I内的运动时间为.求:
(1)粒子的比荷;
(2)磁场区域I和II的宽度d;
(3)速度为v0的粒子从Ol到DD′所用的时间.
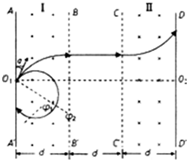
(1)若速度小于某一值时粒子不能从BB′离开区域I,只能从AA′边离开区域I.则无论粒子速度大小,在区域I中运动的时间相同.轨迹如图所示(图中只画了一个粒子的轨迹).则粒子在区域I内做圆周运动的圆心角为φ=300°,
由 Bqv=m T=
得:粒子做圆周运动的周期T=.
由t0=T=
解得:=.
所以粒子的比荷为 =.
(2)速度为v0时粒子在区域I内运动时间为,设轨迹所对圆心角为φ2.
由t0=φ1 =φ2
得:φ2=φ1=60°.
所以其圆心在BB′上,穿出BB′时速度方向与BB′垂直,其轨迹如图所示,
设轨道半径为R,由qv0B=m
得:R==v0 d=Rsin60°=.
磁场区域I和II的宽度d为.
(3)区域I、II宽度相同,则粒子在区域I、II中运动时间均为,
穿过中间无磁场区域的时间为t′==,
则粒子从O1到DD′所用的时间t=+.
所以速度为v0的粒子从Ol到DD′所用的时间为 +.