问题
问答题
设f’(x)在[0,+∞)上单调减少,且
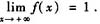
证明级数
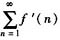 收敛。
收敛。
答案
参考答案:由拉格朗日中值定理知
f(n)-f(n-1)=f’(ξ1),f(n+1)-f(n)=f’(ξ2),
其中n-1<ξ1<n<ξ2<n+1,由于f’(x)单调减少,所以
f(n+1)-f(n)=f’(ξ2)<f’(n)<f’(ξ1)=f(n)-f(n-1)。 (*)
在(*)中令n→∞,由夹逼定理知[*]故对任意的n有[*]从而级数[*]为正项级数。
由(Ⅰ)及正项级数的比较判别法知级数[*]收敛。