问题
问答题
设随机变量(X，Y)的联合概率密度为
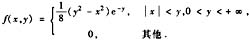
讨论随机变量X和Y的相关性和独立性。
答案
参考答案：为判断独立性，需再求Y的边缘密度
[*]
由于fx(x)·fy(y)≠f(x，y)，故X，Y不独立
又[*]
所以cov(X，Y)=EXY-EX·EY=0，从而可知X与Y既不独立，也不相关。
搜题请搜索小程序“爱下问搜题”
设随机变量(X，Y)的联合概率密度为
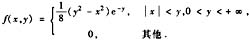
讨论随机变量X和Y的相关性和独立性。
参考答案：为判断独立性，需再求Y的边缘密度
[*]
由于fx(x)·fy(y)≠f(x，y)，故X，Y不独立
又[*]
所以cov(X，Y)=EXY-EX·EY=0，从而可知X与Y既不独立，也不相关。