问题
选择题
在半径为R的圆形区域内有垂直于纸面向内的匀强磁场，磁感应强度为B，一质量为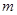
、电荷量为
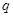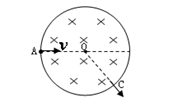
的负电荷，以速率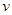
从A点垂直于磁场方向正对着磁场的圆心射入后从C点射出，已知角AOC为1200，则该粒子在磁场中的运动时间为：（ ）
A．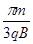
B．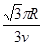
C．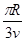
D．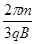
答案
AB
分析：带电粒子在磁场中由洛伦兹力提供向心力，使粒子做匀速圆周运动．从而可推导出轨道半径公式与周期公式，由题中运动的时间与磁感应强度可求出粒子的比荷，由于圆磁场的半径未知，所以无法求出轨道半径，也不能算出粒子的初速度．
解答：解：带电粒子在洛伦兹力作用下做匀速圆周运动，则有：Bqv=m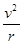
由几何关系可得：R=rtan30°
再由周期公式可得：T=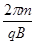
，而运动时间为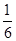：t=
T=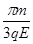
或者t=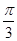
×
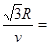
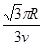
故选：AB．
点评：带电粒子在磁场中运动的题目解题步骤为：定圆心、画轨迹、求半径，同时还利用圆弧的几何关系来帮助解题．值得注意是圆形磁场的半径与运动轨道的圆弧半径要区别开来．