问题
问答题
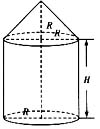
如图,一个容积为V(单位:立方米)的粮仓,它的顶部是高与底圆半径都是R(单位:米)的圆锥形顶棚,底部是半径为R的圆形地基,侧面是高与底圆半径分别是H(单位:米)与R的圆柱面形的围墙,若每平方米地基与每平方米围墙的造价是每平方米顶棚造价的两倍,求使粮仓造价最便宜的H与R。
答案
参考答案:由题设知粮食的容积
[*]
若每平方米顶棚的造价为k元,则粮仓的总造价为
[*]
找题目要求,应求函数W(R,H)在条件[*]之下的最小值点,由于函数W(R,H)与函数[*]有同样的最小值点,从而可引入如下的拉格朗日函数
[*]
F(R,H,λ)的驻点满足
[*]
从以上第二式可得[*]代入第一式可得[*]再由第三式即可求出驻点是
[*]
因驻点唯一,且实际问题必有最低的造价,故当H与R分别取上面所求得的值时,粮仓的造价最便宜。
[*]
