问题
问答题
如图15-4-6所示，场强为E的匀强电场和磁感应强度为B的匀强磁场相互正交，一个质子以速度v0以跟E、B都垂直的方向从A点射入.质子质量为m，电荷量为e，当质子运动到c点时，偏离入射方向的距离为d.则质子在c点的速率为多大？
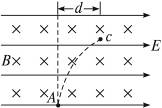
图15-4-6
答案
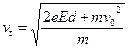
质子的运动过程：因为洛伦兹力不做功，不会改变速度的大小，而电场力始终做正功，会使质子速度增大，洛伦兹力和电场力的合力的大小、方向都在不断变化，质子必然做变加速曲线运动.
应用什么规律来解答呢？牛顿第二定律和运动学公式，都要求是匀变速，从上面的分析知道质子运动过程不满足动量定理，F合t=mv t-mv 0要求F是恒力，或者可用平均力替代，此题F合大小方向时刻在变，F合无法求得，而且公式中的时间t也无法求出，公式也是对直线运动才可用代数法去直接运算，所以也不行；动能定理ΔE k=W，即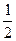
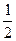mvt2-mv02=W1+W 2，不需做直线运动，不涉及时间，洛伦兹力的功为零，电场力的功计算时不计路径，W电=eEd，所以可用.因而有：
eEd=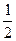mvt2-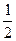mv02,解得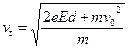
电势能减少量：ΔE=eUAC=eEd
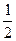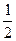动能增量：ΔEk=mvt2-mv02
由能量守恒定律知：ΔE减=Ek
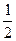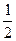则ΔE=ΔEk，eEd=mvt2-mv02
所以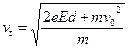.