问题
问答题
如图15-5-25所示，一半径为R的绝缘圆筒中有沿轴线方向的匀强磁场，磁感应强度为B，一质量为m、带电荷量为q的正粒子(不计重力)以速度为v从筒壁的A孔沿半径方向进入筒内，设粒子和筒壁的碰撞无电荷量和能量的损失，那么要使粒子与筒壁连续碰撞，绕筒壁一周时恰好又从A孔射出，问：
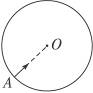
图15-5-25
(1)磁感应强度B的大小必须满足什么条件？
(2)粒子在筒中运动的时间为多少？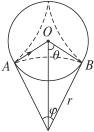
答案
(1)B=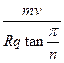
(n=3,4,5,…)
(2) 
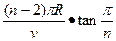(n=3,4,5,…)
(1)粒子射入圆筒后受洛伦兹力作用而偏转，设第一次与B点碰撞，碰后速度方向又指向O点，假设粒子与筒壁撞n-1次，运动轨迹是n段相等的圆弧，再从A孔射出.
设第一段圆弧的圆心为O′，半径为r，如图所示(n=3的情景)，
则θ=2π/2n=π/n
由几何关系有：r=Rtan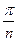
又r=mv/Bq，故
B=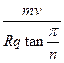(n=3,4,5,…).
(2)粒子运动的周期T=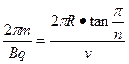
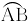所对的圆心角φ=2(
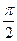-θ)=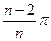
粒子从A→B用的时间
t′=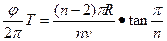
粒子运动的总时间
t=nt′=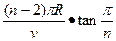 (n=3,4,5,…).