(22分)在一个放射源水平放射出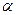 、
、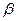 和
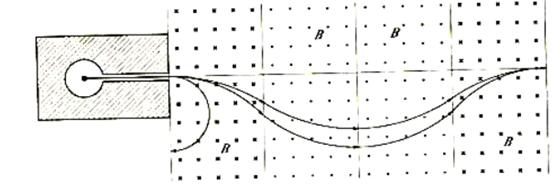
和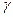 三种射线,垂直射入如图所示磁场。区域Ⅰ和Ⅱ的宽度均为d,各自存在着垂直纸面的匀强磁场,两区域的磁感强度大小B相等,方向相反(粒子运动不考虑相对论效应)。
三种射线,垂直射入如图所示磁场。区域Ⅰ和Ⅱ的宽度均为d,各自存在着垂直纸面的匀强磁场,两区域的磁感强度大小B相等,方向相反(粒子运动不考虑相对论效应)。
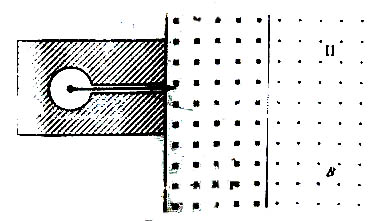
(1)若要筛选出速率大于v1的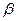 粒子进入区域Ⅱ,要求磁场宽度d与B和v1的关系。
粒子进入区域Ⅱ,要求磁场宽度d与B和v1的关系。
(2)若B=0.0034T,V1=0.1c(c是光速度),则可得d; 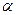 粒子的速率为0.001c,计算
粒子的速率为0.001c,计算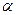 和
和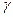 射线离开区域Ⅰ时的距离;并给出
射线离开区域Ⅰ时的距离;并给出 去除
去除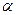 和
和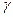 射线的方法。
射线的方法。
(3)当d满足第(1)小题所给关系时,请给出速率在;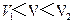 区间的
区间的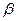 粒子离开区域Ⅱ时的位置和方向。
粒子离开区域Ⅱ时的位置和方向。
(4)请设计一种方案,能使离开区域Ⅱ的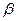 粒子束在右侧聚焦且水平出射。
粒子束在右侧聚焦且水平出射。
已知:电子质量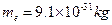 ,
,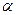 粒子质量
粒子质量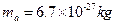 ,电子电荷量
,电子电荷量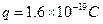 ,
,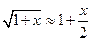 (
(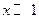 时)
时)
(1)
(2) ,
, ,可用薄纸挡去a粒子,须用厚铅板挡掉γ射线。
,可用薄纸挡去a粒子,须用厚铅板挡掉γ射线。
(3)速率在 区间射出的β粒子速宽为
区间射出的β粒子速宽为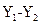 ,方向水平向右。
,方向水平向右。
(4)由对称性可以设计出如图所示的磁场区域,最后形成聚焦,且方向水平向右。

(1)根据带电粒子在磁场中受洛伦磁力作用后作圆周运动的规律
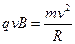 ①
①
由临界条件d、B和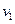 的关系为
的关系为
 ②
②
(2)由①式可得a粒子的回旋半径
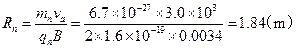
由②式得
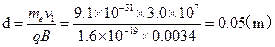
竖直方向的距离为

可见通过区域Ⅰ的磁场难以将a粒子与γ射线分离。可用薄纸挡去a粒子,须用厚铅板挡掉γ射线。
(3)在上述磁场条件下,要求速率在 区间的β粒子离开Ⅱ时的位置和方向。先求出速度为
区间的β粒子离开Ⅱ时的位置和方向。先求出速度为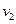 的β粒子所对应的圆周运动半径
的β粒子所对应的圆周运动半径
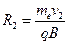
该β粒子从区域Ⅰ磁场射出时,垂直方向偏离的距离为
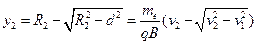
同理可得从区域Ⅱ射出时,垂直方向偏离的距离为
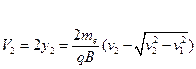
同理可得,与速度为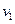 对应的β粒子垂直方向偏离的距离为
对应的β粒子垂直方向偏离的距离为
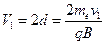
速率在 区间射出的β粒子速宽为
区间射出的β粒子速宽为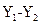 ,方向水平向右。
,方向水平向右。
(4)由对称性可以设计出如图所示的磁场区域,最后形成聚焦,且方向水平向右。