问题
计算题
（16分）如图所示，在xoy平面内第二象限的某区域存在一个矩形匀强磁场区，磁场方向垂直xoy平面向里，边界分别平利于x轴和y轴。一电荷量为e、质量为m的电子，从坐标原点为O以速度v0射入第二象限，速度方向与y轴正方向成45°角，经过磁场偏转后，通过P（0，a）点，速度方向垂直于y轴，不计电子的重力。
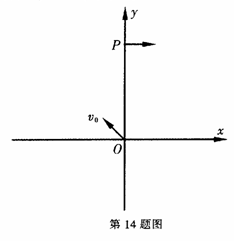
（1）若磁场的磁感应强度大小为B0，求电子在磁场中运动的时间t；
（2）为使电子完成上述运动，求磁感应强度的大小应满足的条件；
（3）若电子到达y轴上P点时，撤去矩形匀强磁场，同时在y轴右侧加方向垂直xoy平面向里的匀强磁场，磁感应强度大小为B1，在y轴左侧加方向垂直xoy平面向里的匀强电场，电子在第（k+1）次从左向右经过y轴（经过P点为第1次）时恰好通过坐标原点。求y轴左侧磁场磁感应强度大小B2及上述过程电子的运动时间t。
答案
解：（1）如图甲所示，
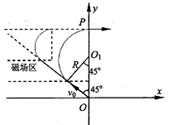
电子在磁场中转过的角度θ=3π/4。
运动周期T=2πm/eB0。t=θT/2π，联立解得t=3πm/4eB0。
（2）设磁感应强度最小值为Bmin，对应的最大回旋半径为R，圆心O1.则有，ev0Bmin=m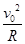
，R+
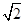R=a
联立解得：Bmin=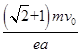
。
磁感应强度的大小应满足的条件为：B≥。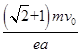
（3）设电子在y轴右侧和左侧做圆周运动的半径分别为r1和r2，则有，
ev0B1=m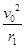
，ev0B2=m
，
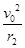由图乙的几何关系可知，
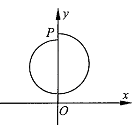
2k(r1-r2)=a
联立解得：B2=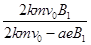
。
设电子在y轴右侧和左侧做圆周运动的周期分别为T1和T2，则有，
T1=2πm/eB1，T2=2πm/eB2。
t=k(T1+T2)/2
联立解得，t=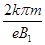
-
。
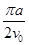画出带电粒子在磁场中运动的轨迹图，应用洛伦兹力等于向心力、图中几何关系及其相关知识列方程解答。