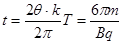问题
计算题
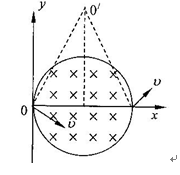
(2012年2月天水一中检测)如图所示，圆形区域的匀强磁场，磁感应强度为B、方向垂直纸面向里，边界跟y轴相切于坐标原点O。 O点处有一放射源，沿纸面向各方向射出速率均为v的某种带电粒子，带电粒子在磁场中做圆周运动的半径是圆形磁场区域半径的两倍。已知该带电粒子的质量为m、电量为q，不考虑带电粒子的重力。
（1）推导粒子在磁场空间做圆周运动的轨道半径；
（2）求粒子通过磁场空间的最大偏转角；
（3）若粒子与磁场边界碰撞后以原速率反弹，则从O点沿x轴正方向射入磁场的粒子第一次回到O点经历的时间是多长？（已知arctan2=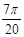
）
答案
（1）
（2）
（3）
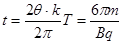
（1）带电粒子进入磁场后，受洛仑兹力作用，由牛顿第二定律得：
， 。
（2）设粒子飞出和进入磁场的速度方向夹角为φ，
则 
x是粒子在磁场内轨迹的两端点的直线距离。
x最大值为2R，对应的就是φ最大值.，由题述2R=r
所以
（3）设粒子与边界相邻两次碰撞过程通过的弧长所对的圆心角为2θ，该弧长所对磁场边界圆的圆心角为2β。如图所示。
则tan
=
， =
，
由图中的几何关系，可得θ+β=π/2，
=
要使粒子还能通过O点，应满足
（
均为正整数）
即
（均为正整数）
当粒子第一次回到O点，应取
又α粒子在磁场中做匀速圆周运动的周期
所以从O点沿x轴正方向射出的粒子第一次回到O点经历的时间是