问题
计算题
(18分)如图所示，光滑的绝缘平台水平固定，在平台右下方有相互平行的两条边界MN与PQ，其竖直距离为h=1.7m，两边界间存在匀强电场和磁感应强度为B=0.9T且方向垂直纸面向外的匀强磁场，MN过平台右端并与水平方向呈θ=37°．在平台左端放一个可视为质点的A球，其质量为mA=0.17kg，电量为q=+0.1C，现给A球不同的水平速度，使其飞出平台后恰好能做匀速圆周运动．g取10m/s2．
(1)求电场强度的大小和方向；
(2)要使A球在MNPQ区域内的运动时间保持不变，则A球的速度应满足的条件？(A球飞出MNPQ区域后不再返回)
(3)在平台右端再放一个可视为质点且不带电的绝缘B球，A球以vA0=3m/s的速度水平向右运动，与B球碰后两球均能垂直PQ边界飞出，则B球的质量为多少？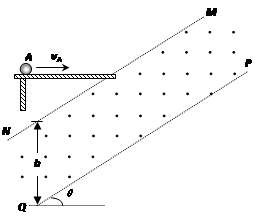
答案
(1)A球能做圆周运动，必须有：Eq=mAg…
…
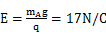电场强度方向竖直向上…
(2)A球在MNPQ区域运动时间相等，必须从边界MN飞出，
如图所示，
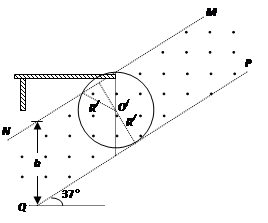
最大半径满足：R/cosθ+R/=hcosθ…
A球做匀速圆周运动有：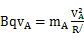
…
解得：vA=0.4m/s…
依题意，A球速度必须满足：0＜vA≤0.4m/s…
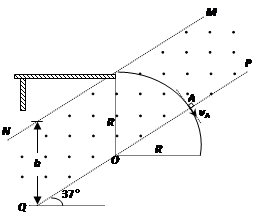
(3)AB相碰后，A做匀速圆周运动，半径R=h…
由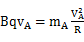
得vA=0.9m/s…
B球做平抛运动，设飞行的水平距离为x，时间为t，有：
x=vB0t…
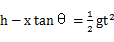……1分
vB0=vytanθ=gttanθ…
得vB0=3m/s…
由动量守恒定律得：
mAvA0=mAvA+mBvB0…
mB=0.119kg…