问题
计算题
如图所示，在一底边长为2L，θ＝45°的等腰三角形区域内(O为底边中点)有垂直纸面向外的匀强磁场. 现有一质量为m，电量为q的带正电粒子从静止开始经过电势差为U的电场加速后，从O点垂直于AB进入磁场，不计重力与空气阻力的影响.
（1）粒子经电场加速射入磁场时的速度？
（2）磁感应强度B为多少时，粒子能以最大的圆周半径偏转后打到OA板？
（3）增大B，可延长粒子在磁场中的运动时间，求粒子在磁场中运动的极限时间.(不计粒子与AB板碰撞的作用时间，设粒子与AB板碰撞前后，电量保持不变并以相同的速率反弹)
答案
（1）
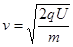
（2） 
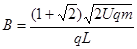
（3） 
⑴粒子经电场加速射入磁场时的速度为v
由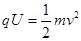 
（3分）
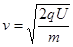得 （2分）
⑵要使圆周半径最大，则粒子的圆周轨迹应与AC边相切，设圆周半径为R
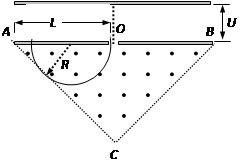
由图中几何关系：
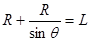（3分）
由
（2分）
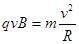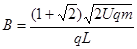得 （2分）
⑶设粒子运动圆周半径为r，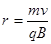 
，当r越小，最后一次打到AB板的点越靠近A端点，在磁场中圆周运动累积路程越大，时间越长. 当r为无穷小，经过n个半圆运动，最后一次打到A点. 有：
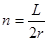（1分）
圆周运动周期：
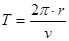（2分）
最长的极限时间
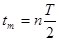（1分）
得：
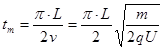（2分）