已知过原点O作函数f(x)=ex(x2-x+a)的切线恰好有三条,切点分别为(x1,y1),(x2,y2),(x3,y3),且x1<x2<x3.
(Ⅰ)求实数a的取值范围.
(Ⅱ)求证:x1<-3.
(Ⅰ)f′(x)=ex(x2+x+a-1),
设切点为(x0,y0),则切线方程为:y-ex0(x02-x0+a)=ex0(x02+x0+a-1)(x-x0),
代入(0,0)得x03+ax0-a=0,
由题意知满足条件的切线恰有三条,
则方程x3+ax-a=0有三个不同的解.(2分)
令g(x)=x3+ax-a,g′(x)=3x2+a.
当a≥0时,g′(x)≥0,g(x)是(-∞,+∞)上增函数,则方程x3+ax-a=0有唯一解.(3分)
当a<0时,由g′(x)=0得x=±
,g(x)在(-∞,-- a 3
)和(- a 3
,+∞)上是增函数,- a 3
在(--
,a 3
)上是减函数- a 3
要使方程x3+ax-a=0有三个不同的根,
只需g(-
)>0- a 3 g(
)<0.- a 3
(5分)(-
)3-a(- a 3
)-a>0- a 3 (
)3+a- a 3
-a<0.- a 3
解得a<-
.(6分)27 4
(Ⅱ)∵g(x)=x3+ax-a,x→∞g(x)→∞g(-
)>0,- a 3
由函数连续性知-∞<x1<-
,(8分)- a 3
∵a<-
,∴g(-3)=-27-4a>0,(10分)27 4
且-3<-
,∴x1<-3.(12分)-a 3

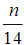 是一个整数。 ()
是一个整数。 ()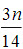 也是一个整数;
也是一个整数;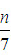 也是一个整数。
也是一个整数。