如图所示，有一半径为R1=1m的圆形磁场区域，圆心为O，另有一外半径为R2=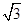
m、内半径为R1的同心环形磁场区域，磁感应强度大小均为B=0.5T，方向相反，均垂直于纸面，一带正电粒子从平行极板下板P点静止释放，经加速后通过上板小孔Q，垂直进入环形磁场区域，已知点P、Q、O在同一竖直线上，上极板与环形磁场外边界相切，粒子比荷q/m=4×107C/kg，不计粒子的重力，且不考虑粒子的相对论效应，求：
（1）若加速电压U1＝1.25×102V，则粒子刚进入环形磁场时的速度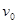
多大？
（2）要使粒子不能进入中间的圆形磁场区域，加速电压U2应满足什么条件？
（3）若改变加速电压大小，可使粒子进入圆形磁场区域，且能水平通过圆心O，最后返回到出发点，则粒子从Q孔进入磁场到第一次经过O点所用的时间为多少？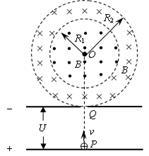
⑴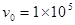
m/s…（2）
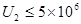（3）t≈1.83×10-7s…
⑴（4分）粒子在匀强电场中，由动能定理得：
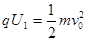……………①……（2分）
解得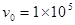：m/s……………②……（2分）
⑵（8分）粒子刚好不进入中间圆形磁场的轨迹如图所示，在RtΔQOO1中有：
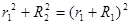.……....③（2分）
解得r1=1m… …④………（1分）
由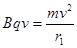
… …⑤………（1分）
得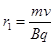 
又由动能定理得：
......…⑥………（2分）
由以上④⑤⑥联立得
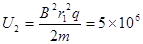V……⑦……（1分）
所以加速电压U2满足条件是
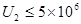V………⑧…（1分）
⑶（7分）
粒子的运动轨迹如图所示，由于 OO3Q共线且竖直，又由于粒子在两磁场中的半径相同，有：O2O3=2O2Q=2r2
由几何关系得∠AO2O3=600，故粒子从Q孔进入磁场到第一次经过圆心O所用的时间
t=(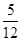
T+
T)=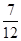 
T…………⑨………（3分）
又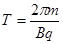
………⑩ ………（2分）
由⑨⑩得t≈1.83×10-7s…………⑾………（2分）
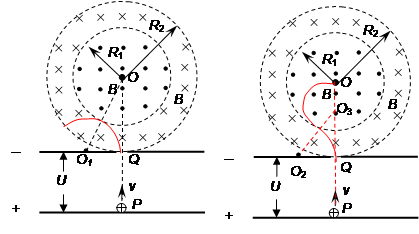
本题考查带电粒子在磁场中的运动，加速后的速度可根据动能定理得出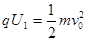，解出加速后的速度。粒子刚好不进入中间圆形磁场的轨迹如图所示，根据几何知识可解出运动半径，结合动能定理，可得出加速电压。粒子的运动轨迹如图所示，由于 OO3Q共线且竖直，又由于粒子在两磁场中的半径相同，有：O2O3=2O2Q=2r2，由几何关系得∠AO2O3=600，可解出粒子从Q孔进入磁场到第一次经过圆心O所用的时间，然后根据公式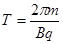算出周期，即可求出时间。