问题
计算题
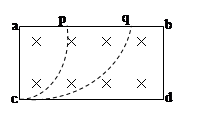
(8分)如图所示，在矩形abcd区域内存在着匀强磁场，两个不同带电粒子从顶角c处沿cd方向射入磁场，分别从p、q两处射出。已知cp连线和cq连线与ca边分别成30°和60°角，不计两粒子的重力。
（1）若两粒子的比荷相同，求两粒子在磁场中运动的时间之比；
（2）若两粒子比荷不同，但都是由静止经同一电场加速后进入磁场的，求两粒子在磁场中运动的速率之比。
答案
（1）
（2）
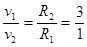
题目分析：（1）设C—>P时间为t1，对应圆心角为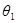
C—>q为t2，对应圆心角为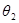
∵
∴
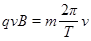
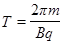又∵
∴T1=T2
由图分析可知：
∴
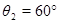
（2）设C—>P粒子的轨道半径为R1
C—>q粒子的轨道半径为R2
ca=d R1+R1·sin30°=d R2-R2·sin30°=d
∴
∴
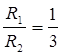
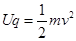
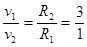
点评：带电粒子以一定的速度进入匀强磁场，在洛伦兹力的作用下做匀速圆周运动．粒子在磁场中运动的周期仅与粒子的比荷有关，而运动的时间与偏转角有关．当入射速度越大时，运动轨道的半径越大，而向心加速度由速度与半径来确定．．