问题
选择题
已知x,y,z都是大于0且小于1的实数,则x(1-y)+y(1-z)+z(1-x)的值( )
A.大于1
B.等于1
C.小于1
D.大于或等于1
答案
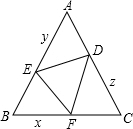
如图,作边长为1的等边三角形,
设BF=x,AE=y,CD=z,
则S△BEF=
BF•BE=1 2
x•1 2
(1-y)=3 2
x(1-y),3 4
同理:S△AED=
y(1-z),3 4
S△CDF=
z(1-x),3 4
S△ABC=
×1×1 2
=3 2
,3 4
∵S△BEF+S△AED+S△CDF<S△ABC,
∴
x(1-y)+3 4
y(1-z)+3 4
z(1-x)<3 4
,3 4
∴x(1-y)+y(1-z)+z(1-x)<1.
故选C.