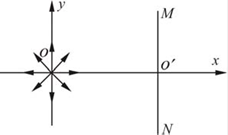
如图所示,在直角坐标系的原点O 处有一放射源,向四周均匀发射速度大小相等、方向都平行于纸面的带电粒子。在放射源右侧有一很薄的挡板,垂直于x 轴放置,挡板与xoy 平面交线的两端M、N 正好与原点O 构成等边三角形,O′ 为挡板与x 轴的交点。在整个空间中,有垂直于xoy 平面向外的匀强磁场(图中未画出),带电粒子在磁场中沿顺时针方向做匀速圆周运动。已知带电粒子的质量为m,带电荷量大小为q,速度大小为υ,MN 的长度为L。(不计带电粒子的重力及粒子间的相互作用)
(1)确定带电粒子的电性;
(2)要使带电粒子不打在挡板上,求磁感应强度的最小值;
(3)要使MN 的右侧都有粒子打到,求磁感应强度的最大值。(计算过程中,要求画出各临界状态的轨迹图)
(1)正电荷 (2) (3)
(3)
题目分析:根据带电粒子在磁场中沿顺时针方向做匀速圆周运动,利用左手定则可判断出粒子带正电荷。
带电粒子在匀强磁场中运动,利用洛伦兹力公式等于向心力和图中几何关系列方程解答。


(1)由左手定则可得,粒子带正电荷。
(2)设磁感应强度大小为B,带电粒子运动的轨迹半径为r,带电粒子做圆周运动的向心力由洛仑兹力提供,有: 得
得
 ①
①
由于从O点射出的粒子的速度大小都相同,由上式可知,所有粒子的轨迹半径都相等。
由几何知识可知,为使粒子不打在挡板上,轨迹的半径最大值为 ②
②
由①②两式可得,磁感应强度的最小值
3)为使MN的右侧都有粒子打到,打在N点的粒子最小半径的轨迹为图乙中的圆弧OMN,图中点O3为轨迹的圆心,由于内接△OMN为正三角形,
由几何知识,最小的轨迹半径为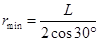
粒子做匀速圆周运动的向心力由洛仑兹力提供,有
所以,磁感应强度的最大值
点评:对带电粒子在磁场中匀速圆周运动的求解,关键是画出匀速圆周运动的轨迹,利用几何知识找出圆心及相应的半径,从而找出圆弧所对应的圆心角.由圆心和轨迹用几何知识确定半径是研究带电粒子在匀强磁场中做匀速圆周运动的重要方法.