问题
解答题
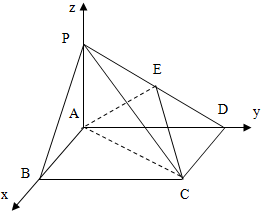
如图，在底面是矩形的四棱锥P-ABCD中，PA⊥平面ABCD，PA=AB=2，BC=4．E是PD的中点，
（1）求二面角E-AC-D的余弦值；
（2）求直线CD与平面AEC所成角的正弦值．
答案
以A为原点，AB所在直线为x轴，AD所在直线为y轴，AP所在直线为z轴建立空间直角坐标系，则A（0，0，0），B（2，0，0），C（2，4，0），D（0，4，0），
E（0，2，1），P（0，0，2）．
∴
=（2，0，0），AB
=（0，4，0），AD
=（0，0，2），AP
=（-2，0，0），CD
=（0，2，1），AE
=（2，4，0）．AC
（1）设平面AEC的法向量
=（x，y，z），令z=1，则n
=（x，y，1）．n
由
即
•n
=0AE
•n
=0AC
，解得2y+1=0 2x+4y=0
∴x=1 Y=- 1 2
=（1，-n
，1）．1 2
平面ABC的法向量
=（0，0，2）．AP
cos＜
，n
=AP＞
=
•n AP |
|•|n
|AP
=2
×23 2
．2 3
所以二面角E-AC-D所成平面角的余弦值是
．2 3
（2）因为平面ABC的法向量是
=（1，-n
，1），而1 2
=（-2，0，0）．CD
所以cosθ=
=
•n CD |
|•|n
|CD
=--2
×23 2
．2 3
直线CD与平面AEC的正弦值
．2 3