问题
证明题
在正三棱锥P-ABC中,三条侧棱两两互相垂直,G是△PAB的重心,E、F分别为BC、PB上的点,且BE:EC= PF:FB=1:2.求证:平面CEF⊥平面PBC.
答案
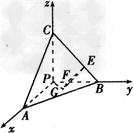
证明:如图,以三棱锥的顶点P为原点,以PA、PB、PC所在直线分别为x轴、y轴、z轴建立空间直角坐标系
令PA=PB=PC=3,
则A(3,0,0),B(0,3,0),C(0,0,3),E(0,2,1),F(0,1,0),G(1,1,0),P(0,0,0).
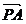 =(3,0,0),
=(3,0,0),
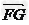 =(1,0,0),
=(1,0,0),
故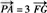 ,
,
∴PA∥FG.
而PA⊥平面PBC,
∴FG⊥平面PBC.
又FG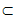 平面EFG,
平面EFG,
∴平面GEF⊥平面PBC.

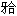 位置。3个月前因
位置。3个月前因 慢性牙髓炎做根管治疗及充填治疗。临床检查示:两侧咬肌、颞肌有触压痛,两侧TMJ无弹响、无压痛,
慢性牙髓炎做根管治疗及充填治疗。临床检查示:两侧咬肌、颞肌有触压痛,两侧TMJ无弹响、无压痛,