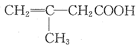问题
解答题
已知函数f(x)=ax3-
(1)当a>2时,求函数f(x)的极小值; (2)试讨论曲线y=f(x)与x轴的公共点的个数. |
答案
(1)f′(x)=3ax2-3(a+2)x+6=3a(x-
)(x-1)2 a
∵a>2,∴
<12 a
∴当x<
或x>1时,f'(x)>0;2 a
当
<x<1时,f'(x)<02 a
∴f(x)在(-∞,
),(1,+∞)内单调递增,在(2 a
,1)内单调递减2 a
故f(x)的极小值为f(1)=-a 2
(2)①若a=0,则f(x)=-3(x-1)2
∴f(x)的图象与x轴只有一个交点.
②若a<0,则
<1,2 a
∴当x<
或x>1时,f'(x)<0,2 a
当
<x<1时,f'(x)>02 a
∴f(x)的极大值为f(1)=-
>0a 2
∵f(x)的极小值为f(
)<02 a
∴f(x)的图象与x轴有三个公共点.
③若0<a<2,则
>1.2 a
∴当x<1或x>
时,f'(x)>0,2 a
当
<x<1时,f'(x)<02 a
∴f(x)的图象与x轴只有一个交点
④若a=2,则f'(x)=6(x-1)2≥0
∴f(x)的图象与x轴只有一个交点
⑤当a>2,由(1)知f(x)的极大值为f(
)=-4(2 a
-1 a
)2-3 4
<0,函数图象与x轴只有一个交点.3 4
综上所述,若a≥0,f(x)的图象与x轴只有一个公共点;
若a<0,f(x)的图象与x轴有三个公共点.