问题
填空题
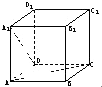
已知正方体ABCD-A1B1C1D1的棱长为1,则直线DA1与AC间的距离为______.
答案
设n=λ
+μAB
+AD
是A1D和AC的公垂线段上的向量,AA1
则n•
=(λA1D
+μAB
+AD
)•(AA1
-AD
)=μ-1=0,∴μ=1.AA1
又n•
=(λAC
+μAB
+AD
)•(AA1
+AB
)=λ+μ=0,∴λ=-1.AD
∴n=-
+AB
+AD
.故所求距离为AA1 3 3
d=
=|AA1•|
•n|AA1 |n|
|=-
+AB
+AD AA1 3
=1 3
;3 3
故答案为
.3 3
