问题
问答题
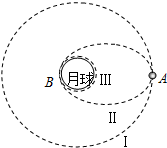
在“嫦娥探月”工程中,假设月球半径为R,月球表面的重力加速度为g0,飞船在半径为4R的圆形轨道Ⅰ运动,到达轨道的A点点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B再次点火进入月球近月轨道Ⅲ绕月球作圆周运动.求:
(1)飞船在轨道Ⅰ上的运行速率;
(2)飞船在A点处点火后瞬间与点火前相比,速度是变大还是变小?
(3)飞船在轨道Ⅲ绕月球运行一周所需的时间.
答案
(1)设月球的质量为M,飞船的质量为m,飞船绕月运动速度为V,飞船绕月运动向心力为F,
=mGMm (4R)2 v2 4R
=mg0GMm R2
解得:v=1 2 g0R
(2)飞船在半径为4R的圆形轨道Ⅰ运动,到达轨道的A点时点火变轨进入椭圆轨道Ⅱ是做逐渐靠近地心的运动,要实现这个运动必须万有引力大于飞船所需向心力,所以应给飞船减速,减小所需的向心力.
(3)设飞船在轨道Ⅲ绕飞船在轨道月球运行一周所需的时间为T,此时重力充当向心力
则mg0=m
R4π2 T2
T=2πR g0
故飞船在轨道Ⅲ绕月球运行一周所需的时间为2πR g0
答:(1)飞船在轨道Ⅰ上的运行速率是1 2
;g0R
(2)飞船在A点处点火后瞬间与点火前相比是变小.
(3)飞船在轨道Ⅲ绕月球运行一周所需的时间是2π
.R g0
