(16分)如图所示,在矩形区域ABCD内有垂直于纸面向外的匀强磁场,磁感应强度大小为B=5.0×10—2T,矩形区域AD长为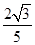 m,AB宽为0.2 m,在AD边中点O处有一放射源,某时刻,放射源沿纸面向磁场中各方向均匀地辐射出速率均为v=2×l06 m/s的某种带正电粒子,带电粒子质量m=1.6×10-27 kg,电荷量为q=+3.2×l0-19C(不计粒子重力),求:
m,AB宽为0.2 m,在AD边中点O处有一放射源,某时刻,放射源沿纸面向磁场中各方向均匀地辐射出速率均为v=2×l06 m/s的某种带正电粒子,带电粒子质量m=1.6×10-27 kg,电荷量为q=+3.2×l0-19C(不计粒子重力),求:

(1)带电粒子在磁场中做圆周运动的半径;
(2)从BC边界射出的粒子中,在磁场中运动的最短时间;
(3)分别从BC边界和CD边界射出粒子数目的比值。
(1)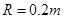 (2)
(2)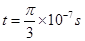 (3)
(3)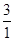
题目分析:(1)粒子进入匀强磁场,洛伦兹力提供向心力即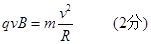
得: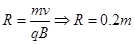 (1分)
(1分)
(2)因为所有粒子的轨迹半径相同,所以弦最短的圆所对应的圆心角最小,运动时间最短
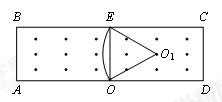
作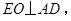 EO弦最短(1分)
EO弦最短(1分)
∵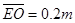 ,且
,且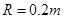
所以对应的圆心角为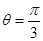 (1分)
(1分)
∵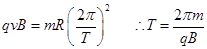 (2分)
(2分)
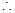 最短时间为:
最短时间为: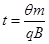 ,∴
,∴ 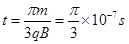 (1分)
(1分)
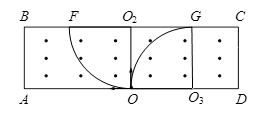
(3) 如图所示,沿OA射入的粒子从F点射出,为左边界;沿OO2射入的粒子轨迹与BC切点为右边界,所以从BC边界射出的粒子分布在图示FG区域,
故从BC边射出粒子射入时分布的夹角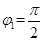 (2分)
(2分)
粒子从CD边界射出区域如下图所示
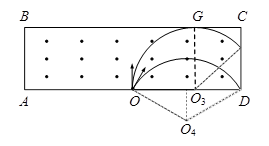
从D点射出粒子与AD成夹角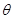 ,
,
∵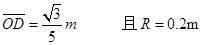
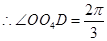 (2分)
(2分)
此时射入磁场的粒子速度方向与AD夹角为 (1分)
(1分)
当轨迹圆与BC相切时,为能从CD边射出磁场的最上边缘的粒子
该粒子进入磁场速度方向垂直AD向上,与OD边的夹角为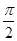
故从CD边界射出的粒子分布的夹角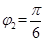 (1分)
(1分)
故从两边界射出粒子的比例为 (2分)
(2分)

 A
A A
A