问题
计算题
(16分)如图所示的直角坐标系第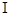
、
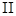象限内存在方向向里的匀强磁场，磁感应强度大小B=0.5T，处于坐标原点O的放射源不断地放射出比荷
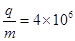C/kg的正离子，不计离子之间的相互作用。
⑴求离子在匀强磁场中运动周期；
⑵若某时刻一群离子自原点O以不同速率沿x轴正方向射出，求经过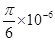
s时间这些离子所在位置构成的曲线方程；
⑶若离子自原点O以相同的速率v0=2.0×106m/s沿不同方向射入第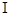象限，要求这些离子穿过磁场区域后都能平行于y轴并指向y轴正方向运动，则题干中的匀强磁场区域应怎样调整（画图说明即可）？并求出调整后磁场区域的最小面积。
答案
（1）π×10-6s （2）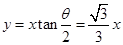
（3）
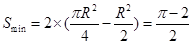
题目分析：⑴根据牛顿第二定律 有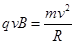 
２分
运动周期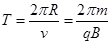
２分
⑵离子运动时间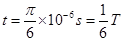
２分
根据左手定则，离子沿逆时针方向作半径不同的圆周运动，
转过的角度均为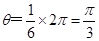
１分
这些离子所在位置均在过坐标原点的同一条直线上，
该直线方程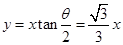 ２分
⑶离子自原点O以相同的速率v0沿不同方向射入第一象限磁场，均做逆时针方向的匀速圆周运动
根据牛顿第二定律 有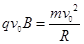
２分
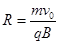
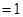ｍ １分
这些离子的轨道圆心均在第二象限的四分之一圆弧AC上，欲使离子穿过磁场区域后都能平行于y轴并指
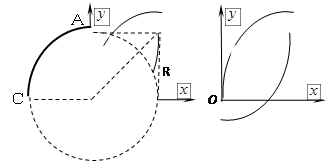
向y轴正方向运动，离开磁场时的位置在以点（１，０）为圆心、半径Ｒ＝１m的四分之一圆弧（从原点Ｏ起顺时针转动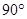
）上，磁场区域为两个四分之一圆的交集，如图所示 ２分
调整后磁场区域的最小面积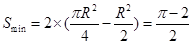m2 ２分