问题
问答题
要发射一颗人造地球卫星,使它在半径为r2的预定轨道上绕地球做匀速圆周运动,为此先将卫星发射到半径为r1的近地暂行轨道上绕地球做匀速圆周运动.如图所示,在A点,使卫星速度增加,从而使卫星进入一个椭圆的转移轨道上,当卫星到达转移轨道的远地点B时,再次改变卫星速度,使它进入预定轨道运行,试求卫星从A点到B点所需的时间.已知地球表面的重力加速度大小为g,地球的半径为R.
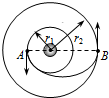
答案
卫星在轨道r1时,万有引力提供圆周运动向心力:G
=mr1mM r 21
①4π2 T2
因为物体m'在地球表面有重力等于万有引力:G
=mg,mM R2
可得:GM=gR2 ②
由①②可得:T1=2πr1 R
③r1 g
当卫星在椭圆轨道运行:其半长轴为:r3=
④r1+r2 2
依开普勒第三定律:
=r 31 T12
得:r 33 T32
T3=T1r 33 r 31
代入③④得:T3=π(r1+r2) R r1+r2 2g
故卫星从A到B的时间tAB=
T3=1 2 π(r1+r2) 2R r1+r2 2g
答:卫星从A到B的时间为π(r1+r2) 2R
.r1+r2 2g
