问题
解答题
(本小题满分12分)
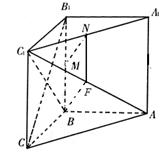
在直三棱柱ABC—A1B1C1中,∠ABC=90°,BC=CC1,M、N分别为BB1、
A1C1的中点.
(1)求证:CB1⊥平面ABC1;
(2)求证:MN//平面ABC1.
答案
详见解析
题目分析:(1)根据直三棱柱的性质,利用面面垂直性质定理证出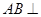 平面
平面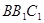 ,得出
,得出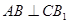 .正方形
.正方形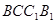 中,对角线
中,对角线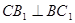 ,由线面垂直的判定定理可证出
,由线面垂直的判定定理可证出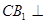 平面
平面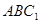 ;(2)取
;(2)取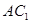 的中点
的中点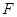 ,连
,连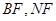 ,利用三角形中位线定理和平行四边形的性质,证出
,利用三角形中位线定理和平行四边形的性质,证出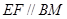 且
且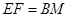 ,从而得到
,从而得到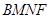 是平行四边形,可得
是平行四边形,可得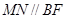 ,结合线面平行判定定理即可证出
,结合线面平行判定定理即可证出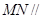 面
面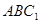 .
.
解:(1)在直三棱柱ABC—A1B1C1中,
侧面BB1C1C⊥底面ABC,且侧面BB1C1C∩底面ABC=BC,
∵∠ABC=90°,即AB⊥BC,
∴AB⊥平面BB1C1 2分
∵CB1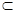 平面BB1C1C,∴AB⊥CB1. 4分
平面BB1C1C,∴AB⊥CB1. 4分
∵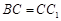 ,
,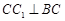 ,∴
,∴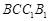 是正方形,
是正方形,
∴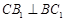 ,∴CB1⊥平面ABC1. 6分
,∴CB1⊥平面ABC1. 6分
(2)取AC1的中点F,连BF、NF. 7分
在△AA1C1中,N、F是中点,∴NF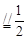 AA1,又∵BM
AA1,又∵BM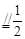 AA1,∴EF
AA1,∴EF BM, 8分
BM, 8分
故四边形BMNF是平行四边形,∴MN//BF, 10分
而EF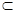 面ABC1,MN
面ABC1,MN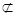 平面ABC1,∴MN//面ABC1 12分
平面ABC1,∴MN//面ABC1 12分