某市道路改造工程，如果让甲工程队单独工作，需要30天完成，如果让乙工程队单独工作，则需要60天方可完成；甲工程队施工每天需付施工费2.5万元，乙工程队施工每天需付施工费1万元．请解答下列问题：
（1）甲、乙两个工程队一起合作几天就可以完成此项工程？
（2）甲、乙两个工程队一起合作10天后，甲工程队因另有任务调离，剩下的部分由乙工程队单独做，请问共需多少天才能完成此项工程？
（3）如果要使整个工程施工费不超过65万元，甲、乙两个工程队最多能合作几天？
（4）如果工程必须在24天内（含24天）完成，你如何安排两个工程队施工，才能使施工费最少？请说出你的安排方法，并求出所需要的施工费．
解：（1）设甲、乙两个工程队一起合作x天就可以完成此项工程，
依题意得：（
）x=1，
解得：x=20．
答：甲、乙两个工程队一起合作20天就可以完成此项工程；
（2）设完成这项道路改造工程共需y天，
依题意得：
×10+
×y=1，
解得y=40．
答：完成这项道路改造工程共需40天；
（3）因为甲工程队单独完成工程需2.5×30=75万元，
乙工程队单独完成工程需1×60=60万元，
要想使施工费尽可能少，甲工程队要少参与，
即合作的时间要尽可能少，剩下的由乙单独完成，
设甲、乙两个工程队合作a天，
则由题意可知乙工程队还需单独做（60﹣3a）天，
得：（1+2.5）a+1×（60﹣3a）≤65，
0.5a+60﹣3a≤65，
解得：a≤10．
答：甲、乙两个工程队最多能合作10天；
（4）由题意知，甲、乙两个工程队单独做都不可能在规定时间内完成，必须合作，
又甲工程队单独完成工程需2.5×30=75万元，
乙工程队单独完成工程需1×60=60万元，
75>60，
因而应安排乙工程队在工程期限内尽可能多做，
即做满24天．
设应安排他们合作m天，
由题意可得：
m+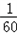
×24=1，
解得：m=18．
即安排甲、乙两工程队合作18天，剩下的部分乙工程队单独做6天．
施工费为：2.5×18+1×24=69（万元）．