问题
计算题
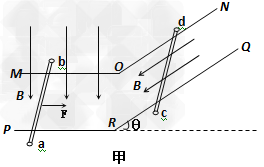
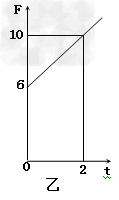
如图甲，电阻不计的轨道MON与PRQ平行放置，ON及RQ与水平面的倾角θ=53°，MO及PR部分的匀强磁场竖直向下，ON及RQ部分的磁场平行轨道向下，磁场的磁感应强度大小相同，两根相同的导体棒ab和cd分别放置在导轨上，与导轨垂直并始终接触良好。棒的质量m=1.0kg，R=1.0Ω，长度与导轨间距相同，L=1.0m，棒与导轨间动摩擦因数μ=0.5，现对ab棒施加一个方向向右，大力随乙图规律变化的力F的作用，同时由静止释放cd棒，则ab棒做初速度为零的匀加速直线运动，g取10m/s2，求：
(1)ab棒的加速度大小；
(2)磁感应强度B的大小；
(3)若已知在前2s内外力做功W=30J，求这一过程中电路产生的焦耳热；
(4)求cd棒达到最大速度所需的时间。
答案
解：(1)对ab棒：f=μmg，v=at
F-BIL-f=ma
F=m(μg+a)+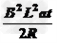
①
a=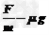
=1m/s2
(2)当t=2s时，F=10N 由①
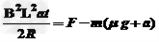
B=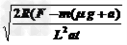
=2T
(3)0-2s过程中，对a、b棒，由动能定理知：
x=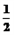
at2=2m，v=at=2m/s
W-μmgx-Q=
mv2
Q=18J
(4)当时间为t时，cd棒平衡，速度最大
N′=BIL+mgcos53°
f=μN′
mgsin53°=f
mgsin53°=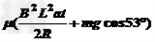
解得：t=5s
