问题
证明题
证明命题“等腰三角形底边上的中点到两腰的距离相等”。 (要求画图，写已知，求证和证明)
答案
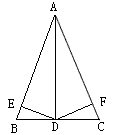
已知：如图，△ABC中，AB=AC，BD=CD，DE⊥AB于E，DF⊥AC于F。 （AB和AC是等腰三角形的2边，BC是底，D是中点）
求证：DE=DF
证明：连结AD ∵AB=AC，BD=CD
∴AD平分∠BAC
∵DE⊥AB于E，DF⊥AC于F
∴DE=DF
搜题请搜索小程序“爱下问搜题”