问题
问答题
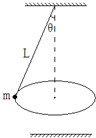
在某星球表面附近,一根长为L的不可伸长的细绳,一端固定,另一端固定一质量为m的小球.小球在水平面内做圆锥摆运动,摆线与竖直方向的夹角为θ,周期为T.仅考虑物体受该星球的引力作用,忽略其他力的影响,已知该星球的半径为R,若发射一颗在距该星球表面距离为R处绕该星球做匀速圆周运动的卫星.求:
(1)该星球表面的重力加速度;
(2)这颗卫星的运行周期T1.
答案
(1)由图可知,小球圆周运动的半径:r=Lcosθ
T=2πr g
g=4π2Lcosθ T2
(2)卫星绕该星球做匀速圆周运动,根据万有引力提供向心力得:
=GMm (R+h)2
,h=Rm?4π2(R+h) T 21
T1=T8R Lcosθ
答:(1)该星球表面的重力加速度是
;4π2Lcosθ T2
(2)这颗卫星的运行周期是T
.8R Lcosθ
