问题
解答题
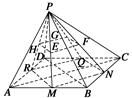
已知ABCD是平行四边形，P点是ABCD所在平面外的一点，连接PA、PB、PC、PD.设点E、F、G、H分别为△PAB、△PBC、△PCD、△PDA的重心.
（1）试用向量方法证明E、F、G、H四点共面；
（2）试判断平面EFGH与平面ABCD的位置关系，并用向量方法证明你的判断.
答案
(1)证明略(2) 平面EFGH∥平面ABCD
（1） 分别延长PE、PF、PG、PH交对边于M、N、Q、R点，因为E、F、G、H分别是所在三角形的重心，所以M、N、Q、R为所在边的中点，顺次连接M、N、Q、R得到的四边形为平行四边形，且有
=
，
=
，
=
，
=
∴
=
+
=（-）+（-）
=
（-）+（-）
=（
+
）
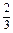
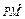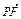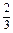
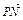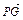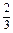
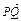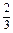
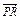
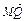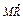
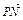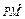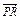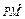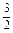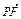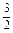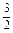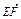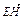又∵=-=-=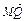
∴=（+）,∴=+
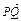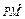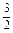
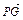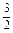
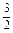
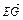
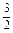
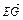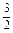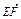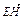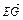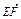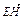
由共面向量定理知：E、F、G、H四点共面.
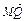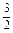
(2) 由（1）得=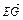,故∥.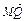
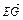又∵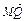
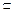平面ABC，EG
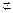平面ABC.
∴EG∥平面ABC.
又∵=-=-=
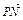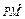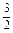
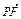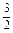
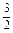
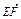
∴MN∥EF，又∵MN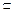平面ABC，EF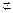平面ABC，
EF∥平面ABC.
∵EG与EF交于E点，
∴平面EFGH∥平面ABCD.
