问题
多选题
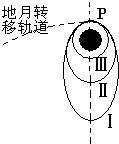
2007年11月5日,“嫦娥一号”探月卫星沿地月转移轨道达到月球,在距月球表面200km的P点进行第一次“刹车制动”后被月球捕获,进入椭圆轨道Ⅰ绕月飞行,如图所示.之后,卫星在P点经过几次“刹车制动”,最终在距月球表面200km、周期127分钟的圆形轨道Ⅲ上绕月球做匀速圆周运动.若已知月球的半径R月和引力常量G,忽略地球对“嫦娥一号”的引力作用,则由上述已知条件知( )
A.可估算月球的质量
B.可估算月球的重力加速度
C.卫星沿轨道Ⅰ经过P点的速度小于沿轨道Ⅲ经过P点的速度
D.卫星沿轨道Ⅰ经过P点的加速度大于沿轨道Ⅱ经过P点的加速度
答案
A、根据万有引力提供圆周运动向心力G
=m(R+h)mM (R+h)2
可以算得月球的质量M,故A正确;4π2 T2
B、根据在月球表面重力和万有引力相等有月球表面重力加速度g=
,在求出月球质量M的前提下可以计算出重力加速度,故B正确;GM R2
C、卫星在轨道III上做匀圆周运动,在轨道I上经P点后做离心运动,根据匀速圆周运动条件和离心运动条件可得,卫星在轨道I上运动的线速度大于在轨道III上经P点的速度,故C错误;
D、卫星的加速度由万有引力产生,根据G
=ma可知,卫星在轨道I和轨道III上经P点时的加速度相同,故D错误mM r2
故选AB.
