问题
问答题
设想宇航员完成了对火星表面的科学考察任务,乘坐返回舱围绕火星做圆周运动的轨道舱.为了安全,返回舱与轨道舱对接时,二者必须具有相同的速度.返回舱在返回过程中需克服火星引力做功W=mgR(1-
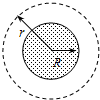
),式中各量分别为:返回舱与人的总质量为m,火星表面重力加速度为g,火星半径为R,轨道舱到火星中心的距离为r,如图所示.不计火星表面大气对返回舱的阻力和火星自转的影响.求:R r
(1)返回舱与轨道舱对接时,返回舱的动能;
(2)该宇航员乘坐的返回舱至少需要获得多少能量,才能返回轨道舱?
答案
(1)设火星的质量为M,轨道舱的质量为m1.在火星表面处有g=GM R2
轨道舱绕火星做圆周运动时,应有G
=m1Mm1 r2 v2 r
对接时,返回舱与轨道舱的速度相等.由以上两式解得v返=v=gR2 r
所以对接时返回舱的动能为Ek=
mv返2=1 2 mgR2 2r
(2)设返回舱返回过程中需要的能量为E,由能量守恒定律知,E-W=Ek,
∵返回舱返回过程克服引力做功W=mgR(1-
)R r
∴E=W+Ek=mgR(1-
)+R r
=mgR(1-mgR2 2r
)R 2r
答:(1)返回舱与轨道舱对接时,返回舱的动能为
;mgR2 2r
(2)该宇航员乘坐的返回舱至少需要获得mgR(1-
)的能量,才能返回轨道舱.R 2r
