问题
单项选择题
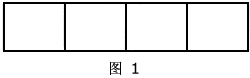
用6种不同的颜色给图1中4个格子涂色，每个格子涂一种颜色，要求相邻的两个格子颜色不同，且两端的格子的颜色也不同，则不同的涂色方法共有( )种。
A．630
B．620
C．610
D．600
E．590
答案
参考答案：A
解析：
[分析]： 四个格子颜色都不相同的涂法共有
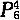＝360(种) 其中恰有两个格子颜色相同的共有
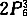＝240(种) 只用两种颜色的涂法共有
＝30(种) 由加法原理，不同的涂色方法共有 360+240+30＝630(种)
