问题
选择题
| 选修4-4:坐标系与参数方程 在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρsin(θ+
(Ⅰ)求C1的直角坐标方程; (Ⅱ)当C1与C2有两个不同公共点时,求实数a的取值范围. |
答案
(Ⅰ)曲线C1的极坐标方程为ρ(
sinθ+2 2
cosθ)=2 2
a,2 2
即ρcosθ+ρsinθ=a,
∴曲线C1的直角坐标方程为x+y-a=0.
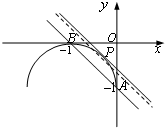
(Ⅱ)曲线的直角坐标方程为(x+1)2+(y+1)2=1(-1≤y≤0),为半圆弧,
如图所示,曲线C1为一组平行于直线x+y=0的直线,
当直线C1与C2相切时,由
=1,得a=-2±|-1-1-a| 2
,2
舍去a=-2-
,则a=-2+2
,2
当直线C1过点A(0,-1)、B(-1,0)两点时,a=-1,
∴由图可知,当-1≤a<-2+
时,曲线C1与曲线C2有两2
个公共点.