问题
填空题
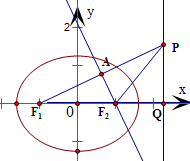
设F1,F2分别是椭圆
|
答案
设准线与x轴的交点为Q,连结PF2,
∵PF1的中垂线过点F2,
∴|F1F2|=|PF2|,可得|PF2|=2c,
∵|QF2|=
-c,且|PF2|≥|QF2|,a2 c
∴2c≥
-c,两边都除以a得2•a2 c
≥c a
-a c
,c a
即2e≥
-e,整理得3e2≥1,解得e≥1 e
,3 3
结合椭圆的离心率e∈(0,1),得
≤e<1.3 3
故答案为:(
,1).3 3