如图所示，在距水平地面高h1＝1.2m的光滑水平台面上，一个质量m＝1kg的小物块压缩弹簧后被锁扣K锁住，储存的弹性势能Ep＝2J。现打开锁扣K，物块与弹簧分离后将以一定的水平速度向右滑离平台，并恰好从B点沿切线方向进入光滑竖直的圆弧轨道BC。已知B点距水平地面的高h2＝0.6m，圆弧轨道BC的圆心O，C点的切线水平，并与水平地面上长为L＝2.8m的粗糙直轨道CD平滑连接，小物块沿轨道BCD运动并与右边的竖直墙壁会发生碰撞，重力加速度g＝10m/s2，空气阻力忽略不计。试求：
（1）小物块运动到B的瞬时速度vB大小及与水平方向夹角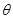
（2）小物块在圆弧轨道BC上滑到C时对轨道压力Nc大小
（3）若小物块与墙壁碰撞后速度反向、大小变为碰前的一半，且只会发生一次碰撞，那么小物块与轨道CD之间的动摩擦因数μ应该满足怎样的条件.
（1）4m/s，60°（2）33.3N（3）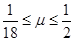
题目分析：⑴解法一:
小物块由A运动到B的过程中做平抛运动，机械能守恒
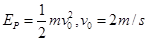（1分）
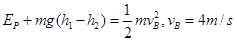（2分）
根据平抛运动规律有：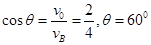
（2分）
解法二:
小物块由A运动到B的过程中做平抛运动，机械能守恒
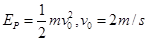（1分）
小物块由A运动到B的过程中做平抛运动，在竖直方向上根据自由落体运动规律可知，
小物块由A运动到B的时间为：
t＝
＝
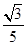s≈0.346s （1分）
根据平抛运动规律有：
tan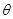
＝
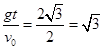， 解得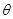：=60° （1分）
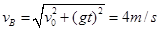（2分）
⑵根据图中几何关系可知，
h2＝R（1－cos∠BOC），解得：R＝1.2m （1分）
根据能的转化与守恒可知，
（2分）
对小球在圆弧轨道C点应用牛顿运动定律
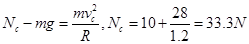（2分）
⑶依据题意知，
①μ的最大值对应的是物块撞墙前瞬间的速度趋于零，根据能量关系有：
mgh1＋Ep＞μmgL 代入数据解得：μ＜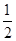
（2分）
②对于μ的最小值求解，首先应判断物块第一次碰墙后反弹，能否沿圆轨道滑离B点，设物块碰前在D处的速度为v2，由能量关系有：mgh1＋Ep＝μmgL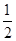＋ mv22
第一次碰墙后返回至C处的动能为：EkC＝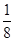
mv22－μmgL 可知即使μ＝0，有：
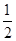mv22＝14J 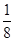mv22＝3.5J＜mgh2＝6J，小物块不可能返滑至B点 （2分）
故μ的最小值对应着物块撞后回到圆轨道最高某处，又下滑经C恰好至D点停止，因此有：
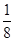mv22≤2μmgL， 联立解得：μ≥
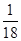（1分）
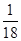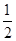综上可知满足题目条件的动摩擦因数μ值：≤μ＜（1分）