问题
填空题
正四棱锥S-ABCD中,O为顶点在底面上的射影,P为侧棱SD的中点,且SO=OD,则直线BC与平面PAC所成的角等于 .
答案
30°
如图,以O为原点建立空间直角坐标系Oxyz.
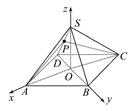
设OD=SO=OA=OB=OC=a,则A(a,0,0),B(0,a,0),C(-a,0,0),
P(0,-
,),
则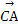
=(2a,0,0),
=(-a,-,),
=(a,a,0).
设平面PAC的法向量为n,可取n=(0,1,1),
则cos<,n>= 
=
=
,
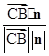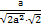∴<,n>=60°,
∴直线BC与平面PAC所成的角为90°-60°=30°.
，达到平衡，加一定量N2气体保持总压力不变，平衡将会（）。