问题
单项选择题
3+2×32+3×33+4×34+…+n×3n=（）。
A.A
B.B
C.C
D.D
答案
参考答案：A
解析：
设Sn=3+2×32+3×33+4×34+…+n×3n
则3Sn=32+2×33+3×34+4×35+…+(n-1)3n+n×3n+1
把以上两式相减，得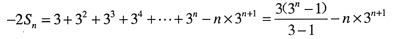
故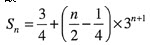
故正确答案为A。
搜题请搜索小程序“爱下问搜题”
3+2×32+3×33+4×34+…+n×3n=（）。
A.A
B.B
C.C
D.D
参考答案：A
解析：
设Sn=3+2×32+3×33+4×34+…+n×3n
则3Sn=32+2×33+3×34+4×35+…+(n-1)3n+n×3n+1
把以上两式相减，得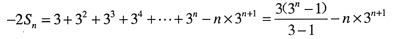
故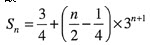
故正确答案为A。