参考答案：C

解析：

由{C_n+1-PC_n}为等比数列知

(C_n+1-PC_n)²=(C_n+2-PC_n+1)(C_n-PC_n-1)

即[2ⁿ⁺¹+3ⁿ⁺¹-P(2ⁿ+3ⁿ)]²=[2ⁿ⁺²+3ⁿ⁺²-P(2ⁿ⁺¹+3ⁿ⁺¹)]×[2ⁿ+3ⁿ-P(2^n-1+3^n-1)]

此式可化为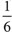(2-P)(3-P)×2n×3n=0

解得P=2或P=3

故正确答案为C。