计划发射一颗距离地面高度为地球半径R0的圆形轨道地球卫星,卫星轨道平面与赤道平面重合,已知地球表面重力加速度为g,
(1)求出卫星绕地心运动周期T
(2)设地球自转周期T0,该卫星绕地旋转方向与地球自转方向相同,则在赤道上某一点的人能连续看到该卫星的时间是多少?
(1)地球对卫星的引力提供卫星做匀速圆周运动的向心力,故有
=mGMm (2R0)2
(2R0)4π2 T2
由于地球的质量未知,而地球表面的重力加速度g已知,
故有
=mgGMm R02
联立以上二式可得卫星绕地心运动周期T=2π
=4π8R0 g R0 g
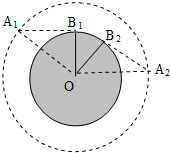
(2)设人在B1位置刚好看见卫星出现在A1位置,最后在B2位置看到卫星从A2位置消失,OA1=2OB1
设∠A1OB1=∠A2OB2=θ
则cosθ=
=OB1 OA1
,1 2
所以θ=π 3
设人从B1位置到B2位置的时间为t,则人转过的角度为
2π,t T0
卫星转过的角度为
2π,t T
故有
+2π 3
2π=t T0
2π,t T
将卫星绕地心运动周期T=2π
代入上式可得8R0 g
t=
=TT0 3(T0-T)
=2π
T08R0 g 3(T0-2π
)8R0 g 4π
T0R0 g 3(T0-4π
)R0 g
答:(1)卫星绕地心运动周期T等于4π
.R0 g
(2)在赤道上某一点的人能连续看到该卫星的时间是
.4π
T0R0 g 3(T0-4π
)R0 g
