问题
问答题
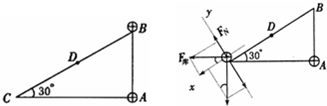
如图所示,一光滑斜面的直角点A处固定一带电量为+q,质量为m的绝缘小球,另一同样小球置于斜面顶点B处,已知斜面长为L,现把上部小球从B点从静止自由释放,球能沿斜面从B点运动到斜面底端C处,
求:(1)小球从B处开始运动到斜面中点D处时的速度?
(2)小球运动到斜面底端C处时,球对斜面的压力是多大?
答案
(1)由题意知:小球运动到D点时,由于AD=AB,所以有 φD=φB
即UDB=φD一φB=0①
则由动能定理得:mg
sin30°+quDB=L 2
mv2-0②1 2
联立①②解得vD=
③gl 2
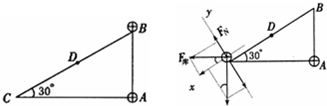
(2)当小球运动到C点时,对球受力分析如图所示则由平衡条件得:
FN+F库•sin30°=mgcos30°④
由库仑定律得:F库=
⑤kq2 (lcos30°)2
联立④⑤得:FN=
mg-3 2 2 3 kq2 L2
由牛顿第三定律即FN'=FN=
mg-3 2 2 3
.kq2 L2
答:(1)小球从B处开始运动到斜面中点D处时的速度为
.gl 2
(2)小球运动到斜面底端C处时,球对斜面的压力是
mg-3 2 2 3
.kq2 L2
