问题
问答题
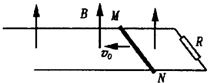
如图所示,有一区域足够大的匀强磁场,磁感应强度为B,磁场方向与水平放置的导轨垂直.导轨宽度为L,右端接有电阻R.MN是一根质量为m的金属棒,金属棒与导轨垂直放置,且接触良好,金属棒与导轨电阻均不计.金属棒与导轨间的动摩擦因数为μ,现给金属棒一水平初速度v0,使它沿导轨向左运动.已知金属棒停止运动时位移为x.求:
(1)金属棒速度为v时的加速度为多大?
(2)金属棒运动过程中通过电阻R的电量q;
(3)金属棒运动过程中回路产生的焦耳热Q.
答案
(1)金属棒速度为v时
产生的感应电动势为E=BLv
感应电流 I=E R
金属棒受到的安培力F=BIL=B2L2v R
根据牛顿第二定律,得
a=
=F+μmg m
+μg=F m
+μgB2L2v mR
(2)金属棒运动过程中通过电阻R的电量q=I•△t
根据法拉弟电磁感应定律
E=
,△φ △t
又I=E R
得到q=φ
=△φ R BLx R
(3)根据能量守恒定律,得
回路产生的焦耳热Q=
m1 2
-μmgxv 20
答:(1)金属棒速度为v时的加速度为
+μgB2L2v mR
(2)金属棒运动过程中通过电阻R的电量为
;BLx R
(3)金属棒运动过程中回路产生的焦耳热Q=
m1 2
-μmgx.v 20
