问题
问答题
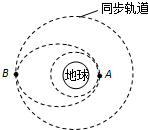
如图 所示,发射地球同步卫星时,可认为先将卫星发射至距地面高度为 h1 的圆形近地轨道上,在卫星经过 A点时点火(喷气发动机工作)实施变轨进入椭圆轨道,椭圆轨道的近地点为 A,远地点为 B.在卫星沿椭圆轨道运动到 B 点(远地点 B 在同步轨道上)时再次点火实施变轨进入同步轨道,两次点火过程都使卫星沿切向方向加速,并且点火时间很短.
已知同步卫星的运动周期为 T,地球的半径为 R,地球表面重力加速度为 g,
求:(计算结果用题目中给出的物理量的符号来表示)
(1)卫星在近地圆形轨道上运动时的加速度大小
(2)同步卫星轨道距地面的高度.
答案
(1)设地球质量为 M,卫星质量为 m,万有引力常量为G
卫星在近地轨道圆运动,由万有引力和牛顿第二定律,有:G
=ma----①mM (R+h1)2
物体在地球表面受到的万有引力等于重力 G
=mg-----②mM R2
由 ①②式联立解得 a=(
)2g R R+h1
(2)设同步轨道距地面高度为h2,由万有引力和牛顿第二定律,有:
G
=m(mM (R+h2)2
)2(R+h2)--③4π T
由②③式联立解得:h2=
-R3 gR2T2 4π2
答:(1)卫星在近地圆形轨道上运动时的加速度大小是(
)2g R R+h1
(2)同步卫星轨道距地面的高度是
-R.3 gR2T2 4π2
