问题
问答题
如图所示，质量m=0.5kg的金属盒AB，放在水平桌面上，它与桌面间的动摩擦因数μ=0.125，在盒内右端B放置质量也为m=0.5kg的长方体物块，物块与盒左侧内壁距离为L=0.5m，物块与盒之间无摩擦．若在A端给盒以水平向右的冲量1.5N·s，设盒在运动中与物块碰撞时间极短，碰撞时没有机械能损失，(g=10m/s2)求：
（1）盒第一次与物块碰撞后各自的速度；
（2）物块与盒的左侧内壁碰撞的次数；
（3）盒运动的时间．
答案
（1）
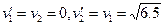="2.55" m/s （2）3次 （3）1.2 s
⑴盒子的初速度为
3 m/s （1分）
设盒子与物块碰撞前的瞬时速度分别为υ1、υ2，根据牛顿第二定
律，盒子的加速度为
=2μg="2.5" m/s （1分）
根据
得
盒子的碰前速度为 
="2.55" m/s （1分）
因物块与盒子之间无摩擦，所以碰前物块速度为v2="0 " （1分）
设碰撞后盒子与物块的瞬时速度分别为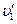
、
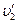，由于碰撞时没有机械能损失，由动量守恒和机械能守恒得
① （2分）
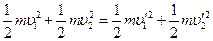② （2分）
由①②解得 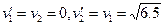="2.55" m/s （2分）
即碰撞后交换速度（另一组解为
，表示碰撞前的状态，舍去）
⑵设盒子在地面上运动的距离为S，盒子的初速度为υ0，由于碰撞没有能量损失，所有盒子与地面摩擦损失的机械能等于系统损失的总机械能，即有
（2分）
解得 
（1分）
盒子每前
进一个L，物块都要与盒子的左侧内壁碰撞一次，由于
，所以物块与盒子的左侧内壁共碰撞3次。（2分）
⑶整个过程中，对盒子应用动量定理得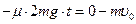 
（2分）
解得 
s＝1.2 s （1分）